This is the third article of the fuzzy logic and machine learning interpretability article series.
In the first article ,we discussed Machine learning interpretability; its definition(s), taxonomy of its methods and its evaluation methodologies.
In the second part of this article series, I introduced basic concepts of fuzzy logic as well as fuzzy inference systems.
This article will build upon the previous ones, and present a new framework that combines concepts from neural networks and fuzzy logic.
. . .
What’s wrong with ANNs?
Artificial neural networks have proved to be efficient at learning patterns from raw data in various contexts. Subsequently, they have been used to solve very complex problems that previously required burdensome and challenging feature engineering (i.e., voice recognition, image classification).
Nonetheless, neural networks are considered black-box, i.e., they do not provide justifications for their decisions (they lack interpretability). Thus, even if a neural network model performs well (e.g., high accuracy) on a task that requires interpretability (e.g., medical diagnosis), it is not likely to be deployed and used as it does not provide the trust that the end-users (e.g., doctors) require.
The problem is that a single metric, such as classification accuracy, is an incomplete description of most real-world tasks.
Neuro-fuzzy modeling
Neuro-fuzzy modeling attempts to consolidate the strengths of both neural networks and fuzzy inference systems.
In the previous article, we saw that fuzzy inference systems, unlike neural networks, can provide a certain degree of interpretability as they rely on a set of fuzzy rules to make decisions (the rule set has to adhere to certain rules to assure the interpretability).
However, the previous article also showed that fuzzy inference systems can be challenging to build. They require domain knowledge, and unlike neural networks, they cannot learn from raw data.
A quick comparison between the two frameworks can be something like this:
- Artificial neural networks: can be trained from raw data, but areblack box
- Fuzzy inference systems: are difficult to train, but can be interpretable
This illustrates the complementarity of fuzzy inference systems and neural networks, and how potentially beneficial their combination can be.
And it is this complementarity that has motivated reasearchers to develop several neuro-fuzzy architectures.
By the end of this article, one of the most popular neuro-fuzzy networks will have been introduced, explained and coded using R.
ANFIS
ANFIS (Adaptive Neuro-Fuzzy Inference System) is an adaptive neural network equivalent to a fuzzy inference system. It is a five-layered architecture, and this section will describe each one of its layers as well as its training mechanisms.
ANFIS architecture as proposed in the orginal article by J-S-R. Jang
Layer 1: Computes memebership grades of the input values
The first layer is composed of adaptive nodes each with a node function:
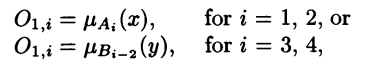
Membership grades
X or y are the input to the node i, Ai and Bi-2 are the linguistic labels (e.g., tall, short) associated with node i, and O1,i is the membership grade of the fuzzy sets Ai and Bi-2. In other words, O1,i is the degree to which the input x (or y) belongs to the fuzzy set associated with the node i.
The membership functions of the fuzzy sets A and B can be for instance the generalized bell function:

Generalized bell function
Where ( ai, bi, ci) constitute the parameter set. As their values change, the shape of the function changes, thus exhibiting various forms of the membership function. These parameters are referred to as the premise parameters.
Layer 2: Compute the product of the membership grades
The nodes in this layer are labeled ∏. Each one of them outputs the product of its input signals.

Output of the second layer
The output of the nodes in this layer represents the firing strength of a rule.
Layer 3: Normalization
This layer is called the normalization layer. Each node i in this layer computes the ratio of the i-th rule’s firing to the sum of all rules’ firing strengths:

Output of the third layer
The outputs of this layer are referred to as the normalized firing strengths.
Layer 4: Compute the consequent part of the fuzzy rules
Every node i in this layer is an adaptive node with a node function:

Output of the fourth layer
Where wi is the normalized firing strength of the i-th rule from layer 3 and (pi, qi, ri) constitute the parameter set of this layer. These parameters are referred to as consequent parameters.
Layer 5: Final output
This layer has a single node which computes the overall output of the network as a summation of all the incoming signals.

Output of the fifth and final layer
Training mechanisms
We have identified two sets of trainable parameters in the ANFIS architecture:
- Premise parameters: (ai, bi, ci)
- Consequent parameters: (pi, qi, ri)
To learn these parameters a hybrid training approach is used. In the forward pass, the nodes output until layer 4 and the consequent parameters are learnt via least-squares method. In the backward pass, the error signals propagate back and premise parameters are learnt using gradient descent.

Table 1: The hybrid learning algorithm used to train ANFIS from ANFIS’ original paper
ANFIS in R
There have been several neuro-fuzzy architectures proposed in the literature. However, the one that was implemented and open-sourced the most is ANFIS.
The Fuzzy Rule-Based Systems (FRBS) R package provides an easy-to-use implementation of ANFIS that can be employed to solve regression and classification problems.
This last section will provide the necessary R code to use ANFIS to solve a binary classification task:
- Install/import the necessary packages
- Import the data from csv to R dataframes
- Set the input parameters required by the frbs.learn() method
- Create and train ANFIS
- Finally, test and evaluate the classifier.
Note that the FRBS implementation of ANFIS is designed to handle regression tasks, however, we can use a threshod (0.5 in the code) to get class labels and thus use it for classification tasks as well!
Conclusion
The apparent complementarity of fuzzy systems and neural networks has led to the development of a new hybrid framework called neuro-fuzzy networks. In this article we saw one of the most popular neuro-fuzzy networks, namely, ANFIS. Its architecture was presented, explained, and its R implementation was provided.
This is the last article of the fuzzy logic and machine learning interpretability article series. I believe that the main takeaways from the three blogs can be:
- Interpretability (in certain contexts) is sometimes of far greater importance than performance.
- There are many ways to assure a certain level of interpretability, one option is to use fuzzy rules to explain the behavior of your machine learning solution.
- Neuro-fuzzy networks are a potential solution to the performance-interpretability tradeoff, it can be worthwhile experimenting with few neuro-fuzzy based architectures.
References
ANFIS: adaptive-network-based fuzzy inference system
This is the second part of the fuzzy logic and machine learning interpretability article series.
In the previous part (here) we discussed Machine learning interpretability; its definition(s), taxonomy of its methods and its evaluation methodologies.
In this second part, we will introduce fuzzy logic and its main components: fuzzy sets, membership functions, linguistic variables, and fuzzy inference systems. These concepts are crucial to understand the use of fuzzy logic in machine learning interpretability.
. . .
Limitations of crisp sets, and the need for fuzzy sets
Classical (or crisp) set theory is one of the most fundamental concepts of mathematics and science. It is an essential tool in various domains, and especially in computer science (e.g., databases, data structures).
Classical set theory relies on the notion of dichotomy: an element x either belongs to a set S or does not. In fact, one of the defining features of a crisp set is that it classifies the elements of a given universe of discourse to members and nonmembers. Crisp sets have clear and unambiguous boundaries.
The belongingness of an element to a set is expressed via a characteristic function.
A characteristic function S(x) of a set S defined on the universe of discourse X has the following form:
(1) S(x)=1 , if x ∈ S and 0 , otherwise
Despite its widespread use, classical set theory still has several drawbacks.
Among them is its incapacity to model imprecise and vague concepts. For instance, let’s say we want to define the set tall people using crisp sets, and we decided to use the following characteristic function:
(2) tallpeople =1 if height>175, 0 otherwise
Meaning that a person is a member of the set of tall people, if their height is greater than 1.75 meters. This definition of the concept of tall leads to unreasonable conclusions. For example, using the characteristic function (2) we deduce that a person whose height is 174.9 cm is not tall, while a person whose height is 175.1 cm is. This sharp transition between inclusion and exclusion sets is one of crisp sets theory’s major flaws, And it is what has led to development and the use of fuzzy sets theory.
Fuzzy logic and fuzzy sets
“As complexity rises, precise statements lose meaning and meaningful statements lose precision”, Lotfi A. Zadeh
Fuzzy logic attempts to resemble the human decision-making process. It deals with vague and imprecise information. Fuzzy logic-based systems have shown great potential in dealing with problems where information is vague and imprecise. They are being used in numerous applications ranging from voice recognition to control.
Fuzzy set theory (introduced in 1965 by Lotfi Zadeh) is an extension of classical set theory. Fuzzy set theory departs from the dichotomy principle and allows for memberships to a set to be a matter of degree. It has gained so much ground because it models better the physical world where most of the knowledge is fuzzy and vague. For example, notions like good, bad, tall, and young are all fuzzy. That is, there is neither a qualitative value, nor a range with clear boundaries that defines them.
Membership functions
Formally, a fuzzy set F is characterized by a membership function mapping the elements of a universe of discourse X to the interval [0, 1].
F :X→0,1
Membership functions map elements of the universe of discourse X to an interval [0,1] where 0 means exclusion, 1 signifies complete membership, and the intermediate membership values show that an element can be a member of two classes at the same time with different degrees. This allows gradual transitions from one class to the other.
The belonging to multiple classes at the same time, and the gradual transition from one class to another, are illustrated in the following example.
Figure 1 shows membership functions of the concept Temperature. In this example, a temperature in celsius can be a member of the following fuzzy sets : Extremely Low, Very low, Low, and Nice temperatures. The X-axis and Y-axis refer respectively to the temperature values in celsius and belongingness percentages. For example, a temperature of 8° is 5% nice and 23% low.
This process of mapping crisp values (such as 8°) to fuzzy values is called Fuzzification. And it is the first step in fuzzy inference systems, more on that later.
Figure 1. Membership functions of the fuzzy sets: extremely low, very low, low, nice temperatures
Linguistic variables
Another fundamental concept of fuzzy logic is linguistic variables. Thanks to linguistic variables (or fuzzy variables), machines can understand the human language, and do inference using our vague and imprecise statements.
A linguistic variable can be defined as a variable whose values are not numbers, but rather, words. Formally, a linguistic variable is defined by the following quintuple:
- X: the name of the variables
- T(X): the set of terms of X
- U: the universe of discourse
- G: the syntactic rule that generates the name of the terms
- µ: the semantic rule that associates each term of X with its meaning
For example, suppose that X is a linguistic variable called Temperature, its set of terms T(X) can be {low, medium, high}, the universe of discourse U can be the interval [-20:55], and the semantic rules are the membership functions of each term.
Fuzzy inference system
Fuzzy sets and linguistic variables allow us to model human knowledge better. However, can machines do inference using the expert knowledge we embedded in them using fuzzy logic?
Fuzzy inference systems do just that.
Given an input and output, a fuzzy inference system formulates a mapping using a set of fuzzy rules (fuzzy rules have the following form If A Then B, where A and B are fuzzy sets).
This mapping allows future decisions to be made and patterns to be discerned in a transparent manner. Fuzzy inference systems are composed of the following components:
- Fuzzifier: converts the crisp input values to fuzzy ones using the membership functions.
- Rule base: stores the fuzzy rules
- Inference engine: performs the fuzzy inference process
- Defuzzifier: transfers the fuzzy inference results into a crisp output.
Figure 2. Main components of a fuzzy inference system.
There are mainly two groups of fuzzy inference systems: Mamdani, and Sugeno (TSK). The difference between the two lies in the consequent part of their fuzzy rules. The consequent part of the Mamdani fuzzy inference system is a fuzzy set. Meanwhile, the consequence of the TSK fuzzy inference system is a mathematical function. This allows the latter to have more predictive power, and the former to have more interpretability.
Example of a fuzzy inference system
To better understand what a fuzzy inference system is, and what it does, let’s discuss the following example of a Mamdani based fuzzy inference system.
We will try to build a fuzzy inference system that takes as input a temperature value, and adjusts the temperature of the Air Conditioner (AC).
- Rule base and membership functions:
To build a fuzzy inference system, a rule base (i.e., a set of fuzzy rules) and membership functions (defining the fuzzy sets) need to be provided. They are usually provided by domain experts.
For the sake of simplicity, let’s use the membership functions in Figure 1. And let’s suppose that our rule base contains the following three rules:
Rule 1: if Temperature is Very Low or Extremely Low Then AC_Command is Very High
Rule 2: if Temperature is Low Then AC_Command is High
Rule 3: if Temperature is Nice Then AC_Command is Normal
- Fuzzification
The first operation that a fuzzy inference system conducts is fuzzification, i.e., it uses the membership functions to convert the crisp input values to fuzzy values.
If our system receives as input the value x=8°, using the membership functions we defined, this value means that the temperature is 5% nice and 23% low. Formally, this can be written as:
U(x=Low)=0.23
U(x=Nice)=0.05
U(x=Very Low)=0
U(x=Extremely Low)=0
- Rules evaluation:
Having fuzzified the input, we can now evaluate the rules in our rule base.
Rule 1: if Temperature is Very Low (=0) or Extremely Low (=0) Then AC_Command is Very High (=0)
Rule 2: if Temperature is Low (=0.23) Then AC_Command is High (=0.23)
Rule 3: if Temperature is Nice (=0.05) Then AC_Command is Normal (=0.05)
- Aggregation and defuzzification:
Aggregation is the process of unifying the outputs of all rules. The values found in the rule evaluation process (0.05 and 0.23) are projected onto the membership functions of AC_Command (Figure 3). The resulting membership functions of all rule consequent are combined.
Finally, defuzzification is carried out. One popular way to conduct defuzzification is to take the output distribution (blue and orange area in Figure 3) and compute its center of mass. This crisp number would be in our example the appropriate degree of the AC.
Figure 3. membership functions of the fuzzy sets Normal, High, Very High AC command
Conclusion
This article covered the basic notions underlying fuzzy logic. We saw how the need for fuzzy sets emerged, and we briefly discussed what fuzzy sets, membership functions, and linguistic variables are. The most important one of all the concepts we saw in this blog (to understand how fuzzy logic is used in machine learning interpretability) is probably fuzzy inference systems.
In the next article (the final), everything we discussed so far will be brought together (ML interpretability and fuzzy logic) to present and discuss what Neuro-Fuzzy architectures are, and how they can be used to tackle the interpretability-performance tradeoff.
References
Department of Computer Engineering, Sharif University of Technology — Fuzzy logic course
Biosignal Processing and Classification Using Computational Learning and Intelligence- Chapter 8 — Fuzzy logic and fuzzy systems
- A. Kalogirou, “Solar Energy Engineering: Processes and Systems: Second Edition,” Solar Energy Engineering: Processes and Systems: Second Edition, pp. 1–819, 2014, doi: 10.1016/C2011–0–07038–2.
- Zhang et al., “Neuro-Fuzzy and Soft Computing — A Computational Approach to Learning and Artificial Intelligence,” International Review of Automatic Control (IREACO), vol. 13, no. 4, pp. 191–199, Jul. 2020, doi: 10.15866/IREACO.V13I4.19179.
This article will attempt to define interpretability in the context of machine learning. Then, we will highlight the importance of machine learning interpretability and explain why it has gained popularity recently. Further, a taxonomy of machine learning interpretability techniques will be provided. Moreover, an evaluation schema of machine learning interpretability will be presented, and finally, we will discuss the properties of the explanations humans tend to prefer.
. . .
Definition(s) of interpretability
Although the literature on machine learning interpretability has been increasing the past few years, no consensus has been reached yet on its definition. Miller (2017) defines interpretability as the degree to which a human can understand the cause of a decision. Kim (2016) on the other hand, defines interpretability as the degree to which a human can consistently predict a model’s output.
In this article we will adopt the following definition: a model is interpretable if its decisions can be easily understood by humans. In other words, a model M1 is more interpretable than a model M2, if the decisions taken by M1 are easier to understand.
Importance of interpretability
The mere high performance of a machine learning model is not enough to trust its decisions. In fact, as it was pointed out by Dosh-Velez (2017): The problem is that a single metric, such as classification accuracy, is an incomplete description of most real-world tasks. This is especially true when the machine learning model is applied in a critical domain (i.e., domain of application where an error committed by the model could lead to severe consequences). If wrong decisions have severe impacts, then interpretability is a must.
Moreover, the need for interpretable machine learning solutions has now been translated to several Artificial Intelligence related regulations passed by countries around the world. The European Union’s General Data Protection Regulation (GDPR) for example, requires among other things, the transparency of all algorithmic decisions (Principle of Transparency) .
Nonetheless, there are still cases where interpretability is not a requirement. These cases are either when the model is used in a low-risk environment, i.e., an error will not have serious consequences, (e.g. a movie recommender system) or the technique has already been extensively studied and examined (e.g. optical character recognition). According to Doshi-Velez and Kim (2017) the need for interpretability is due to an incompleteness in problem formalization, that is to say that for certain problems it is not enough to get the prediction (the what). The model must also explain how it came to the prediction (the why), because a correct prediction only partially solves the problem.
Finally, and according to the same authors, the interpretability of machine learning models makes the evaluation of the following properties easier:
- Fairness: Ensuring that predictions are unbiased and do not implicitly or explicitly discriminate against protected groups. An interpretable model can tell you why it has decided that a certain person should not get a loan, and it becomes easier for a human to judge whether the decision is based on a learned demographic (e.g. racial) bias.
- Privacy: Ensuring that sensitive information in the data is protected.
- Reliability or Robustness: Ensuring that small changes in the input do not lead to large changes in the prediction.
- Causality: Check that only causal relationships are picked up.
- Trust: It is easier for humans to trust a system that explains its decisions compared to a black box.
Taxonomy of interpretability methods
These methods and techniques can be categorized into four categories: model-agnostic, model-specific, global-interpretability, local-interpretability. The first refer to the set of interpretability techniques that can be applied to any machine learning black-box model, the second to those that can only be applied to one model. The third interpretability methods areconcerned with the overall behavior of the model, and finally the fourth category are methods that are concerned with justifying only one prediction of the model.
A more detailed overview of the categories of machine learning interpretability is provided in the following taxonomy taken from the paper Explainable AI: A Review of Machine Learning Interpretability Methods:
Figure 1: Taxonomy of interpretability methods
Evaluation of interpretability
No consensus exists on how to evaluate the interpretability of a machine learning model. Nonetheless, researchers have made initial attempts to formulate some approaches for evaluation. Doshi-Velez and Kim (2017) propose three main levels for the evaluation of interpretability:
- Application level evaluation (real task):The interpretability method is tested by end-users. For instance, in case the software developed is a fracture detection system with a machine learning component that locates and marks fractures in X-rays. At the application level, radiologists would test the fracture detection software directly to evaluate the model. A good baseline for this is always how good a human would be at explaining the same decision.
- Human level evaluation (simple task):is a simplified application level evaluation. The difference is that these experiments are not carried out with the domain experts, but with laypersons. This makes experiments cheaper (especially if the domain experts are radiologists) and it is easier to find more testers. An example would be to show a user different explanations and the user would choose the best one.
- Function level evaluation (proxy task):does not require humans. This works best when the class of model used has already been evaluated by someone else in a human level evaluation. For example, it might be known that the end users understand decision trees. In this case, a proxy for explanation quality may be the depth of the tree. Shorter trees would get a better explainability score. It would make sense to add the constraint that the predictive performance of the tree remains good and does not decrease too much compared to a larger tree.
Human-friendly explanations
Psychology and cognitive science can be of great help when it comes to discovering what humans consider to constitute a “good explanation”. Indeed, Miller (2017) has carried out a huge survey of publications on explanations, and this subsection builds on his summary.
Good explanations are:
- Contrastive: The importance of contrasting explanations is one of the most important findings of machine learning interpretability. Instead of asking why this prediction was made, we tend to ask why this prediction was made instead of another prediction. Humans tend to ask the question: What would the prediction be if input X had been different?. If a client’s loan application is rejected, they would not care for the reasons that generally lead to a rejection. They would be more interested in the factors in their application that would need to change to get the loan. They would be more interested in knowing the contrast between their application and the would-be-accepted application (Lipton 1990).
- Selected: Explanations do not have to cover the whole list of causes of an event. They only need to select one or two causes from a variety of possible causes as an explanation.
- Social: An explanation is part of an interaction between the explainer and the receiver of the explanation (explainee). The social context should determine the content and nature of the explanations. Psychologists and sociologists can help come up with explanations that fit with the audience targeted by the application.
- Focus on the abnormal: Humans focus more on abnormal causes to explain events (Kahnemann and Tversky, 1981). These are causes that have a small probability to occur. Humans consider these kinds of “abnormal” causes as good explanations.
- Consistent with prior beliefs of the explainee: Humans tend to ignore information that is inconsistent with their prior beliefs (confirmation bias, Nickerson 1998). Explanations are not exempt from this kind of bias. Humans tend to devalue or ignore explanations that do not agree with their prior beliefs.
Conclusion
This article broadly introduced the concept of machine learning interpretability. We saw its definitions, importance, taxonomy, and evaluation methods. In the next article, we will attempt to do the same with fuzzy logic. And in the third article, we will see how fuzzy logic can benefit machine learning interpretability.
References
Christoph Molnar, Interpretable Machine Learning
Miller, Tim. “Explanation in artificial intelligence: Insights from the social sciences.” arXiv Preprint arXiv:1706.07269. (2017)
Kim, Been, Rajiv Khanna, and Oluwasanmi O. Koyejo. “Examples are not enough, learn to criticize! Criticism for interpretability.” Advances in Neural Information Processing Systems (2016)
Doshi-Velez, Finale, and Been Kim. “Towards a rigorous science of interpretable machine learning,” no. Ml: 1–13. http://arxiv.org/abs/1702.08608 ( 2017)
Transparent information, communication and modalities for the exercise of the rights of the data subject
- B. Arrieta et al., “Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI,” Information Fusion, vol. 58, pp. 82–115, Oct. 2019
- v. Carvalho, E. M. Pereira, and J. S. Cardoso, “Machine Learning Interpretability: A Survey on Methods and Metrics,” Electronics 2019, Vol. 8, Page 832, vol. 8, no. 8, p. 832, Jul. 2019, doi: 10.3390/ELECTRONICS8080832
Lipton, Peter. “Contrastive explanation.” Royal Institute of Philosophy Supplements 27 (1990): 247–266
Nickerson, Raymond S. “Confirmation Bias: A ubiquitous phenomenon in many guises.” Review of General Psychology 2 (2). Educational Publishing Foundation: 175. (1998)