This is the third article of the fuzzy logic and machine learning interpretability article series.
In the first article ,we discussed Machine learning interpretability; its definition(s), taxonomy of its methods and its evaluation methodologies.
In the second part of this article series, I introduced basic concepts of fuzzy logic as well as fuzzy inference systems.
This article will build upon the previous ones, and present a new framework that combines concepts from neural networks and fuzzy logic.
. . .
What’s wrong with ANNs?
Artificial neural networks have proved to be efficient at learning patterns from raw data in various contexts. Subsequently, they have been used to solve very complex problems that previously required burdensome and challenging feature engineering (i.e., voice recognition, image classification).
Nonetheless, neural networks are considered black-box, i.e., they do not provide justifications for their decisions (they lack interpretability). Thus, even if a neural network model performs well (e.g., high accuracy) on a task that requires interpretability (e.g., medical diagnosis), it is not likely to be deployed and used as it does not provide the trust that the end-users (e.g., doctors) require.
The problem is that a single metric, such as classification accuracy, is an incomplete description of most real-world tasks.
Neuro-fuzzy modeling
Neuro-fuzzy modeling attempts to consolidate the strengths of both neural networks and fuzzy inference systems.
In the previous article, we saw that fuzzy inference systems, unlike neural networks, can provide a certain degree of interpretability as they rely on a set of fuzzy rules to make decisions (the rule set has to adhere to certain rules to assure the interpretability).
However, the previous article also showed that fuzzy inference systems can be challenging to build. They require domain knowledge, and unlike neural networks, they cannot learn from raw data.
A quick comparison between the two frameworks can be something like this:
- Artificial neural networks: can be trained from raw data, but areblack box
- Fuzzy inference systems: are difficult to train, but can be interpretable
This illustrates the complementarity of fuzzy inference systems and neural networks, and how potentially beneficial their combination can be.
And it is this complementarity that has motivated reasearchers to develop several neuro-fuzzy architectures.
By the end of this article, one of the most popular neuro-fuzzy networks will have been introduced, explained and coded using R.
ANFIS
ANFIS (Adaptive Neuro-Fuzzy Inference System) is an adaptive neural network equivalent to a fuzzy inference system. It is a five-layered architecture, and this section will describe each one of its layers as well as its training mechanisms.
ANFIS architecture as proposed in the orginal article by J-S-R. Jang
Layer 1: Computes memebership grades of the input values
The first layer is composed of adaptive nodes each with a node function:
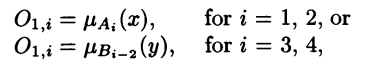
Membership grades
X or y are the input to the node i, Ai and Bi-2 are the linguistic labels (e.g., tall, short) associated with node i, and O1,i is the membership grade of the fuzzy sets Ai and Bi-2. In other words, O1,i is the degree to which the input x (or y) belongs to the fuzzy set associated with the node i.
The membership functions of the fuzzy sets A and B can be for instance the generalized bell function:

Generalized bell function
Where ( ai, bi, ci) constitute the parameter set. As their values change, the shape of the function changes, thus exhibiting various forms of the membership function. These parameters are referred to as the premise parameters.
Layer 2: Compute the product of the membership grades
The nodes in this layer are labeled ∏. Each one of them outputs the product of its input signals.

Output of the second layer
The output of the nodes in this layer represents the firing strength of a rule.
Layer 3: Normalization
This layer is called the normalization layer. Each node i in this layer computes the ratio of the i-th rule’s firing to the sum of all rules’ firing strengths:

Output of the third layer
The outputs of this layer are referred to as the normalized firing strengths.
Layer 4: Compute the consequent part of the fuzzy rules
Every node i in this layer is an adaptive node with a node function:

Output of the fourth layer
Where wi is the normalized firing strength of the i-th rule from layer 3 and (pi, qi, ri) constitute the parameter set of this layer. These parameters are referred to as consequent parameters.
Layer 5: Final output
This layer has a single node which computes the overall output of the network as a summation of all the incoming signals.

Output of the fifth and final layer
Training mechanisms
We have identified two sets of trainable parameters in the ANFIS architecture:
- Premise parameters: (ai, bi, ci)
- Consequent parameters: (pi, qi, ri)
To learn these parameters a hybrid training approach is used. In the forward pass, the nodes output until layer 4 and the consequent parameters are learnt via least-squares method. In the backward pass, the error signals propagate back and premise parameters are learnt using gradient descent.

Table 1: The hybrid learning algorithm used to train ANFIS from ANFIS’ original paper
ANFIS in R
There have been several neuro-fuzzy architectures proposed in the literature. However, the one that was implemented and open-sourced the most is ANFIS.
The Fuzzy Rule-Based Systems (FRBS) R package provides an easy-to-use implementation of ANFIS that can be employed to solve regression and classification problems.
This last section will provide the necessary R code to use ANFIS to solve a binary classification task:
- Install/import the necessary packages
- Import the data from csv to R dataframes
- Set the input parameters required by the frbs.learn() method
- Create and train ANFIS
- Finally, test and evaluate the classifier.
Note that the FRBS implementation of ANFIS is designed to handle regression tasks, however, we can use a threshod (0.5 in the code) to get class labels and thus use it for classification tasks as well!
Conclusion
The apparent complementarity of fuzzy systems and neural networks has led to the development of a new hybrid framework called neuro-fuzzy networks. In this article we saw one of the most popular neuro-fuzzy networks, namely, ANFIS. Its architecture was presented, explained, and its R implementation was provided.
This is the last article of the fuzzy logic and machine learning interpretability article series. I believe that the main takeaways from the three blogs can be:
- Interpretability (in certain contexts) is sometimes of far greater importance than performance.
- There are many ways to assure a certain level of interpretability, one option is to use fuzzy rules to explain the behavior of your machine learning solution.
- Neuro-fuzzy networks are a potential solution to the performance-interpretability tradeoff, it can be worthwhile experimenting with few neuro-fuzzy based architectures.